MCQs Data Structure 60+

1. The operation that combines the element is of A and B in a single sorted array C with n=r+s element is called ….

Where r,s and n is total number of elements in sorted array A,B and c respectively

1. Inserting
2. Mixing
3. Merging
4. Sharing

2. Consider the following functions:

  f(n)   = 2^n
  g(n)   = n!
  h(n)   = n^logn 

Which of the following statements about the asymptotic behavior of f(n), g(n), and h(n) is true?

1. f(n) = O(g(n)); g(n) = O(h(n))
2. (B) f(n) = (g(n)); g(n) = O(h(n))
3. (C) g(n) = O(f(n)); h(n) = O(f(n))
4. (D) h(n) = O(f(n)); g(n) = (f(n))

3. What will be the best case complexity to find the largest element in a sorted array of n elements in term of Big-O notation?

1.  O(n)
2.  O(1)
3. O(logn)
4. O(n/2)

4. The complexity of following code will be:

for(int i=n;i>1; i--){
    for(int j=1; j < n; j*= 2){
        //do constant time stuff
    }
}

1. O((logn)^2)
2. O(2logn)
3.  O(n^2)
4.  O(nlogn)

5. What are the time complexities of finding kth element from beginning and kth element from end in a doubly linked list? Assume n>k, where k is a constant and n is a total number of nodes in the linked list.

1. O(1) and O(n)
2. O(1) and O(1)
3. O(n) and O(1)
4. O(n) and O(n)

6. _____ list is a header list where the node points back to the header node.

1. Doubly header List.
2. Singly header List.
3. Grounder Header List.
4. Circular Header List.

7. Let f(n) and g(n) be asymptotically non-negative functions. Which of the following is correct?

1. θ ( f (n)*g(n)) = min (f (n), g(n))
2. θ ( f (n)*g(n)) = max (f (n), g(n))
3. θ( f (n) + g(n)) = min (f (n), g(n))
4. θ ( f (n) + g(n)) = max (f (n), g(n))

8. For each of the following statements, decide whether it is always true, never true, or sometimes true for asymptotically nonnegative functions f and g. If it is always true or never true, explain why. If it is sometimes true, give one example for which it is true, and one for which it is false.

f(n) = (g(n)) and f(n) = o(g(n))

Ans

Never true: If f(n) = Ω(g(n)) then there exists positive constant cΩ and nΩ such that for all n > nΩ, cg(n) ≤ f(n). But if f(n) = o(g(n)), then for any positive constant c, there exists no(c) such that for all n > no(c), f(n) < cg(n). If f(n) = Ω(g(n)) and f(n) = o(g(n)), we would have that for n > max(nΩ, no(cΩ)) it should be that f(n) < cΩg(n) ≤ f(n) which cannot be.

9. Evaluate the following prefix expression: 1584/3++5/

1. 5
2. 3
3. 4
4. 2

10. Suppose f and l pointers are pointing to first and last nodes of a singly linked list respectively, which of the following operation is dependent on the length of the linked list?

1. Delete the first element
2. Insert a new element as a first element
3. Delete the last element of the list
4. Add a new element at the end of the list

11. How to delete last node from a given linked list, l is pointing last node and t is pointing previous node of last node . (next is pointer part of node)

T->next=l->next
L=t
L->next=t->next
L=null
None of the mentioned

12. If the sequence of operations –push(1),push(2),pop,push(1),push(2),pop,push(2),pop(),pop() are performed on a stack, the sequence of popped out values are

Ans: 2,2,2,1

13. If user try to remove element from the stack data structure which is already empty then it is called as _______

Ans-: Underflow of stack

14. What is preorder traversal of the following binary tree?

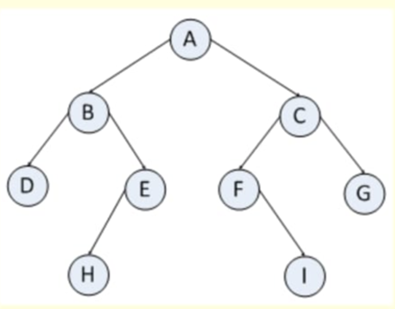
Ans: A,B,D,E,H,C,F,I,G

15. What is inorder traversal of the following binary tree?

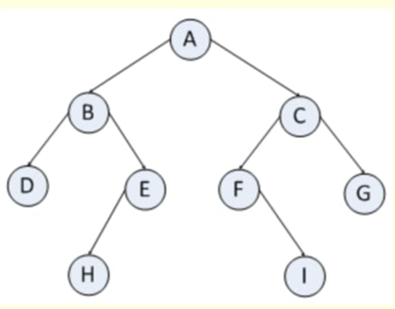
Ans: DBHEAFICG

16. Consider an implementation of unsorted singly linked list. Suppose it has its representation with a head pointer only. Given the representation, which of the following operation can be implemented in O(1) time?

1. Insertion at the front of the linked list
2. Insertion at the end of the linked list
3. Deletion of the front node of the linked list
4. Deletion of the last node of the linked list

Ans: 1,3

17. Consider an implementation of unsorted singly linked list. Suppose ONLY F is pointing to first node of a singly linked list then which of the following operation can be implemented in O(1) time?

1. Insertion at the front of the linked list
2. Insertion at the end of the linked list
3. Deletion of the front node of the linked list
4. Deletion of the last node of the linked list

Ans: 1,3

18. The postfix expression for the following infix expression (A+B)*(C+D)/F+D*E is

Ans: AB+CD+*F/DE*+

19. Construct a binary search tree by inserting the following elements in the order of their occurrence 24,23,22,25,26,46 and 41.What is the postorder traversal of constructed tree.

Ans: 22,23,41,46,26,25,24

20. The preorder traversal sequence of a binary search tree is 10,8,9,13,12. Which one of the following is the postorder traversal sequence of the same tree?

Ans: 9,8,12,13,10

21. Consider the following queue of characters, where QUEUE is a circular array which located six memory cells: FRONT=2, REAR=4, QUEUE: -, A, C, D,-,-(for notation  “-” denotes empty memory cell). What will be the value of front and rear respectively after the following operation? (1)Two letters are deleted (2)three letters x,y,z added to the queue.

Ans: 4 and 1

22. What does the following function do for a given binary tree?

int fun(struct node *root)
{
   if (root == NULL)
       return 0;
   if (root->left == NULL && root->right == NULL)
       return 1;
else
   return fun(root->left) + fun(root->right);
}

Ans: Returns total number of leaf nodes

23. What does the following function value() do for a given binary search tree?

int value(struct node* node){

if (node->left == NULL)

return node->data;

return value(node->left);

}

Ans: Returns node with minimum value

24. What will be postorder traversal of the following binary tree?

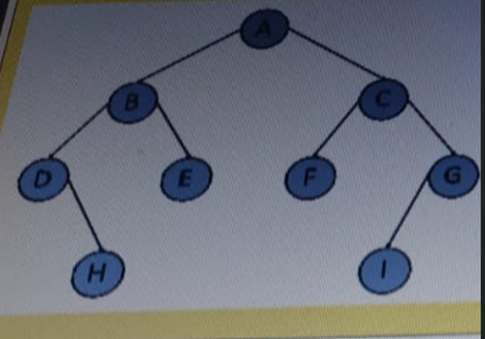
Ans: HDEBFIGCA

25. What does the following function value() do for a given binary search tree?

int value(struct node" node)
  if (node->right = NULL)
    retum node->data,
  return value(node->right);

1. Returns node with minimum value
2. Returns root node always
3. Returns node with maximum value
4. Returns any leaf node always

26. Consider following AVL tree

               60
            /     \
          20      100
                 /   \
               80    120
         

Which of the following updated AVL tree after insertion of 70?

A
        70
      /    \  
    60      100
   /       /    \
 20       80    120 

B
        100
      /    \  
    60      120
   /  \     /  
 20   70   80   


C
        80
      /    \  
    60      100
   /  \       \
 20   70      120

D
        80
      /    \  
    60      100
   /       /   \
 20      70    120  

Ans: c

27. Suppose given function Height() is to calculate the height of a Binary tree. (Where height of a Binary tree is number of nodes along the longest path from the root node to the leaf node.)

int Height(struct node* node){

if (node==NULL)

return 0;

else{

int lHeight = Height(node->left);

int rHeight = Height(node->right);

if (lHeight > rHeight)

return x;

else return Y;

}

}

What should be the values of X and Y so that the function works correctly?

1. X-Height, Y Height
2. X = IHeight, Y = rHeight
3. X = IHeight -1, Y =rHeight – 1
4. X = IHeight+1, Y=rHeight+1

28. Which of the following non linear data structure contains cycle?

1. Stack
2. Queue
3.  Tree
4. Graph

29. Construct a binary search tree by inserting the following elements in the order of their occurrence 36,37,46,45,44,55 and 50. what is postorder traversal of constructed tree?

Ans-: 44,45,50,55,46,37,36

30. How many LR rotation(s) will be applied to construct an AVL tree with given nodes?

30,40,20,50,35,33,15

Ans: 0

31. Consider a min heap, represented by the following

array: 11,31,21,71,41,51,81,91

After inserting a node with value 32, which of the following is the updated min heap?

1. 11,31,21,32,41,51,81,91,71
2. 11, 31, 21, 71, 41, 51, 81, 61, 32
3. 11, 32, 21, 31, 41, 51, 81, 61, 32
4. 32, 11, 31, 21, 71, 41, 51, 81, 61

32. What will be the third move to transfer 3 discs from peg P to peg R with the help of peg Q in Tower of Hanoi problem?

1. Q->R
2. Q->P
3. P->Q
4. R->Q

33. Suppose we are inserting following value in a sequence 10,5,20 and 15 to construct AVL tree .Now suppose we insert 12,which rotation to be carried out to make tree as balance.

Ans: LL

34. The preorder traversal sequence of a binary search tree is 30,20,10,15,25,23,39,35,42.Which one of the following is the postorder traversal sequence of the same tree.

Ans: 15,10,23,25,20,35,42,39,30

35. Suppose we are inserting following value in sequence 20,50,70 and 10 to construct AVL tree. Now suppose we delete 70,which rotation to be performed to make tree as balance?

Ans-: R1

36. Which of the following operations on a max-heap require O(logn) time?

1. Finding the maximum element
2. Inserting any element
3. Inserting an element greater than the maximum element
4. Inserting an element lesser than the minimum element

37. Which traversal gives a sorted sequence in an AVL Tree?

1. inorder
2. preorder
3. postorder
4. levelorder

38. Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap?

1. 25, 12, 16, 13, 10
2. 25, 12, 16, 10, 13
3. 25, 13, 12, 14, 10
4. 25,14,16,13,10

39. What will be the postorder traversal of the AVL tree formed by the nodes given below: 10,15,40,20,50?

Ans: 10,20,50,40,15

40. True statements about AVL tree are

1. It is a binary search tree.
2. Left node and right node differs in height by at most 1 unit
3. Worst case time complexity to search an element is O(logn)
4. Worst case time complexity to search an element is O(n)

Ans: i,ii,iii

41. What is the maximum height of any AVL tree with 7 nodes?(Assume that height of a tree with single node is 1:

1. 2
2. 3
3. 4
4. 5

42. Consider a min heap, represented by the following array: 10,30,20,70,40,50,80,90. After inserting a node with value 33, which of the following is the updated min-heap?

Ans: 10,30,20,33,40,50,80,90,70

43. Consider a hash table of size five ,with starting index zero,and a hash function(x mod 5). Assuming the hash table is initially empty,which of the following is the contents of the table when the sequence 19,32,15,39 is inserted into the table using closed hashing and solving collision using linear probing ? Now that “_” denotes an empty location in the table.

Ans: 15,39,32,_,19

44. Consider a binary min heap implemented using an array. Which one of the following array represents a binary min heap?

1. 10, 40, 45, 20, 30, 25
2. 20, 40, 45, 10, 25, 30
3. 10, 40, 20, 50, 45, 25
4. 10, 45, 20, 40, 50, 25

45. What will be the worst case time complexity for inserts, searches, and deletes in AVL tree?

Ans: O(logn),O(logn) and O(logn) respectively

46. In order to compute the path from vertex I to vertex J in warshall algorithm, we need to find the p[I,J]=__________  for k,I,J=1,2,__,M(Where M in number of nodes in graph)

Ans: P[I,J] OR (P[I,K] AND P[K,J])

Code

let dist be V × V matrix of minimum distances initialized to INFINITY
for each vertex v
  dist[v][v] = 0
for each edge (u, v)
  dist[u][v] = weight(u, v)
 
for k from 0 to |V| – 1
  for i from 0 to |V| – 1
    for j from 0 to |V| – 1
      if (dist[i][k] + dist[k][j]) is less than dist[i][j] then
        dist[i][j] = dist[i][k] + dist[k][j]

47. Consider a hash table of size five ,with starting index zero,and a hash function(x mod 5).

Assuming the hash table is initially empty. What will be the number of collision when the sequence 19,32,15,39 is inserted into the table using closed hashing and solving collision using linear probing?

Ans: 3

48. What is the reason of traversal of a graph using BFS or DFS is different from binary tree traversal ?

1. BFS of a graph uses queue, but postorder traversal of binary tree is recursive
2. DFS of a graph uses stack, but inorder traversal of binary tree is recursive
3. There can be a loop in graph so we must maintain a visited flag for every vertex
4. All of the above

49. Consider a hash table with five slots. The hash function is h(k)=k mod 5. The collisions are resolved by chaining.The following 5 keys are inserted in the order:18,27,13,25,28. The maximum chain lengths in the hash table will be,

Ans: 3

50. The balance factor for an AVL tree is either

Ans-: 0,1 or -1

51. What will be time complexity to find the smallest element in a binary max heap containing n numbers? Ans: O(N)

52. What is/are TRUE statement(s)?

1. Collision occurs when two or more keys produce same hash address
2. Every hash algorithm may produce collision
3. Linear probing is a collision resolution techniques
4. The goal of hashing is to produce a search that takes O(1) time

a only

a and b

a, b and c

a, b, c and d

53. Given the following input (323,335,472,680,989,172) and the hash function x mod 10. The number of collision using linear probing will be ,

Ans: 3

54. In order to compute the shortest path from vertex I to vertex J in Floyd warshall Algorithm, we need to find the p[I,J]=_________ for k,I,J=1,2,__,M.(Where M in number of nodes in graph).

Ans-: MIN(P[I,J],P[I,K]+P[K,J])

# Number of vertices
nV = 4
INF = 999

# Algorithm 
def floyd(G):
    dist = list(map(lambda p: list(map(lambda q: q, p)), G))

    # Adding vertices individually
    for r in range(nV):
        for p in range(nV):
            for q in range(nV):
                dist[p][q] = min(dist[p][q], dist[p][r] + dist[r][q])
    sol(dist)

# Printing the output
def sol(dist):
    for p in range(nV):
        for q in range(nV):
            if(dist[p][q] == INF):
                print("INF", end=" ")
            else:
                print(dist[p][q], end="  ")
        print(" ")

G = [[0, 5, INF, INF],
         [50, 0, 15, 5],
         [30, INF, 0, 15],
         [15, INF, 5, 0]]
floyd(G)

55. Consider a hash table of size five, with starting index zero, and a hash function(x mod 5). Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 17,30,12,19 is inserted into the table using closed hashing and solving collision using linear probing? Now that “_” denotes an empty location in the table.

Ans: 30,_,17,12,19

56. Consider a hash table of size five, with starting index zero, and a hash function(x mod 5). Assuming the hash table is initially empty. What will be the number of collision when the sequence 17,30,12,19   is inserted into the table using closed hashing and solving collision using linear probing?

Ans: 2

57. Which of the following non linear data structure must not have any cycle?

1. Stack
2. Queue
3. Tree
4. Graph

58. Which of the following is best data structure for DFS traversal of a graph?

1. Stack
2. Queue
3. List
4. None of the above

59. Given the following input (321, 333, 470, 678, 988, 170) and the hash function x mod 10, which of the following statements are true?

1. 978, 988 hash to the same value
2.  470, 170 hash to the same value
3.  All elements hash to the same value
4.  Each element hashes to a different value

i only
 
 ii only
 
 i and ii
 
 iii and iv

321 -> 321 mod 10 = 1
333 -> 333 mod 10 = 3
470 -> 470 mod 10 = 0
678 -> 678 mod 10 = 8
988 -> 988 mod 10 = 8
170 -> 170 mod 10 = 0

60. Which of the following is best data structure for the BFS traversal of a graph?

1. Stack
2. Queue
3. Tree
4. Graph

61. Consider a hash table with five slots. The hash function is h(k)=k mod 5. The collisions are resolved by chaining.The following 5 keys are inserted in the order:18,27,13,25,28. The minimum chain lengths in the hash table will be,

Ans: 0

62. Suppose we are inserting following value in a sequence 10,5,20 and 15 to construct AVL tree .Now suppose we insert 18,which rotation to be carried out to make tree as balance.

Ans: LR

62. The complexity of following code will be:

for(int i = 0; i < n; i++)
	 {
		cout << i << endl;               
	}

Ans: O(n)

63. The complexity of following code will be:

for(int i = 0; i < n; i++)
	 {
		cout << i << endl;               
	}

Ans: O(n)

64. The complexity of following code will be:

for(int i = 0; i < 100; i++) 
	{
		for(int j = 0; j < 100; j++)
    {
		//do swap stuff, constant time
		}
	} 

Ans: O(n^2)

65. The complexity of following code will be:

for(int i = 0; i < n; i++) 
	{
		for(int j = 0; j < n; j++)
    {
		//do swap stuff, constant time
		}
	} 

Ans: O(n^2)

66. The complexity of following code will be:

for(int i = 0; i < 2*100; i++)
		 {
		cout << i << endl;
		}

Ans: O(n)

At first you might say that the upper bound is O(2n);
however, we drop constants so it becomes O(n)

67. The complexity of following code will be:

for(int i = 0; i < 2*n; i++)
		 {
		cout << i << endl;
		}

Ans: O(n)

At first you might say that the upper bound is O(2n);
however, we drop constants so it becomes O(n)

68. The complexity of following code will be:

for(int i = 0; i <10 ; i++)
	 {
		cout << i << endl;
	     }

	for(int i = 0; i < 100; i++) 
		{
		for(int j = 0; j < 100; j++)
			{
			//do constant time stuff
			}
		}

Ans: O(n^2)

In this case we add each loop's Big O, in this case n+n^2. O(n^2+n) is not an acceptable answer since we must drop the lowest term. The upper bound is O(n^2). Why? Because it has the largest growth rate

69. The complexity of following code will be:

for(int i = 0; i < n; i++)
	 {
		cout << i << endl;
	     }

	for(int i = 0; i < n; i++) 
		{
		for(int j = 0; j < n; j++)
			{
			//do constant time stuff
			}
		}

Ans: O(n^2)

In this case we add each loop's Big O, in this case n+n^2. O(n^2+n) is not an acceptable answer since we must drop the lowest term. The upper bound is O(n^2). Why? Because it has the largest growth rate

70. The complexity of following code will be:

for(int i = 0; i < 100; i++) 
   {
		for(int j = 0; j < 2; j++)
		{
		//do stuff
		}
   } 

Ans: O(n)

Outer loop is 'n', inner loop is 2, this we have 2n, dropped constant gives up O(n)

71. The complexity of following code will be:

for(int i = 0; i < n; i++) 
	{
		for(int j = 0; j < 2; j++)
		{
		//do stuff
		}
	}

Ans: O(n)

Outer loop is 'n', inner loop is 2, this we have 2n, dropped constant gives up O(n)

72. The complexity of following code will be:

for(int i = 1; i < n; i =i* 2)
	 {
		cout << i << endl;
	}

Ans: O(logn)

There are n iterations, however, instead of simply incrementing, 'i' is increased by 2*itself each run. Thus the loop is log(n).

73. The complexity of following code will be:

for(int i = 1; i < 100; i =i* 2)
	 {
		cout << i << endl;
	}

Ans: O(logn)

There are n iterations, however, instead of simply incrementing, 'i' is increased by 2*itself each run. Thus the loop is log(n).

74. The complexity of following code will be:

for(int i = 0; i < n; i++) 
	{ 
		for(int j = 1; j < n; j *= 2)
			{ 
			//do constant time stuff
			}
	}

Ans: n*log(n)

75. The complexity of following code will be:

While (n>=1)
{ 
	n=n/2;
}

Ans: O(1)

Happy Learning – If you require any further information, feel free to contact me.